В этой статье мы рассмотрим основные преимущества и недостатки использования нейронных сетей для задач машинного обучения. В конце вам станет понятно, когда целесообразно использовать нейронные сети для решения наших задач и при каких обстоятельствах. Мы также узнаем, что не менее важно, когда нам следует избегать использования нейронных сетей и вместо этого отдавать предпочтение другим, более эффективным методам.
Математики будет не много и она будет понятна каждому. Кроме того я буду делать упрощённые выводы для более точного донесения своих мыслей тем, кто вообще не понимает в алгоритмах и нейронных сетях.
Что такое распознавание текста на базе искусственного интеллекта?
Типы нейронных сетей, которые мы обсуждаем сегодня, – это однослойные и глубокие нейронные сети с прямой связью. Эти типы сетей изначально были разработаны для решения задач, для которых методы линейной регрессии не сработали.
В то время, когда разрабатывался прародитель нейронных сетей – так называемый персептрон, регрессионные модели уже существовали и позволяли извлекать линейные зависимости между переменными.
Проблема представления нелинейных взаимосвязей в целом не была разрешима. Затем на сцену вышли многослойные персептроны, которые мы сегодня называем нейронными сетями, и выглядели примерно так:
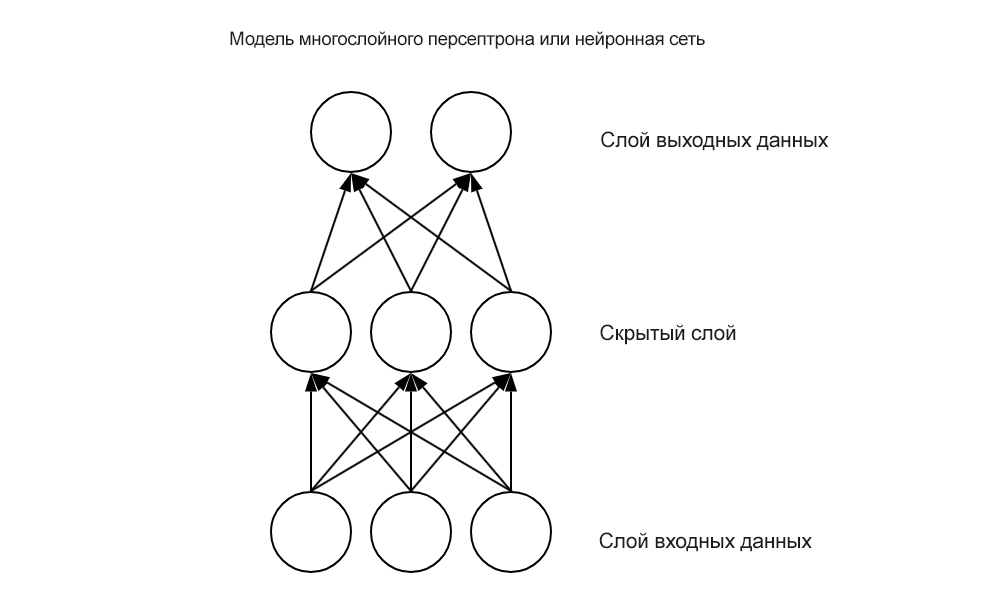
Нейронные сети с прямой связью – это сети узлов, которые передают линейную комбинацию своих входных данных с одного уровня на другой. При этом узлы решают, как модифицировать свои входные данные, используя заданную функцию активации. Функция активации нейрона здесь является ключевой. Выбирая нелинейные функции активации, такие как логистическая функция, показанная ниже, нейронная сеть может внедрять нелинейность в свою работу:

В то время как линейная регрессия позволяет изучать представление линейных задач, нейронные сети с нелинейными функциями активации требуются для нелинейных классов задач.
Таким образом, первым преимуществом нейронных сетей является их гибкость при решении задач с нелинейными формами:
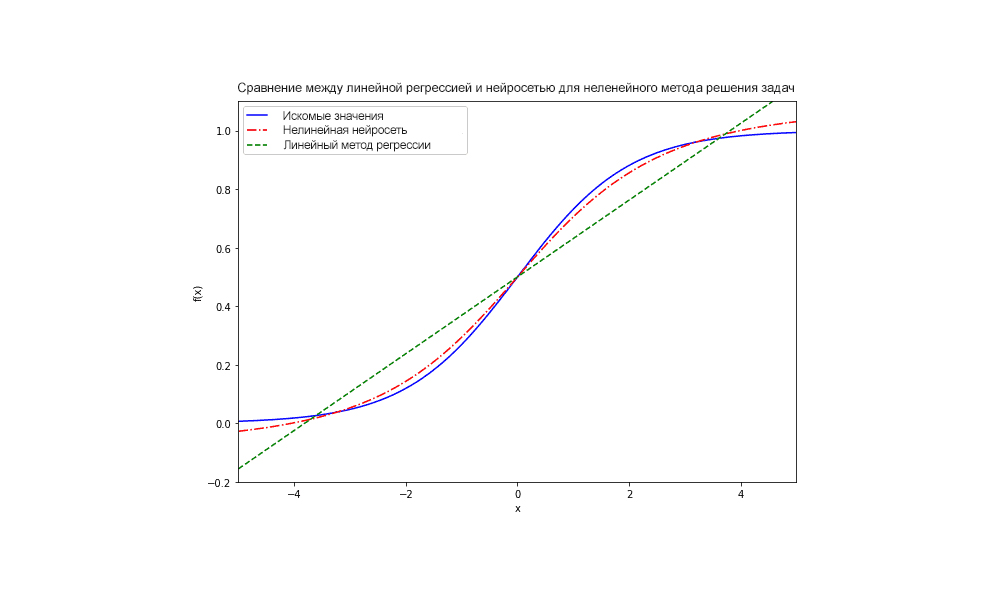
Это означает, что нейронные сети, как правило, можно использовать на предмет решения задачи с областями неизвестных значений, в тот момент когда линейные средства решения не могут дать хоть какой-либо близкий результат.
Теорема об универсальной аппроксимации и ее ограничение
Второе преимущество нейронных сетей связано с их способностью аппроксимировать неизвестные функции, то-есть давать приблизительные, а не точные значения. Это моделирование сложной функции более простой с вычислительной точки зрения функцией.
Основополагающая теорема для нейронных сетей утверждает, что достаточно большая нейронная сеть с одним скрытым слоем может аппроксимировать любые непрерывно дифференцируемые функции.
Если мы знаем, что проблему можно смоделировать с помощью непрерывной функции, тогда, возможно, имеет смысл использовать нейронную сеть для ее решения.
Функция является непрерывной, если ее входные и выходные данные являются непрерывными переменными, и если сама функция четко определена для всех значений своей области. Функция является непрерывно дифференцируемой, если ее производная определена и имеет одно и только одно значение во всей области этой функции:
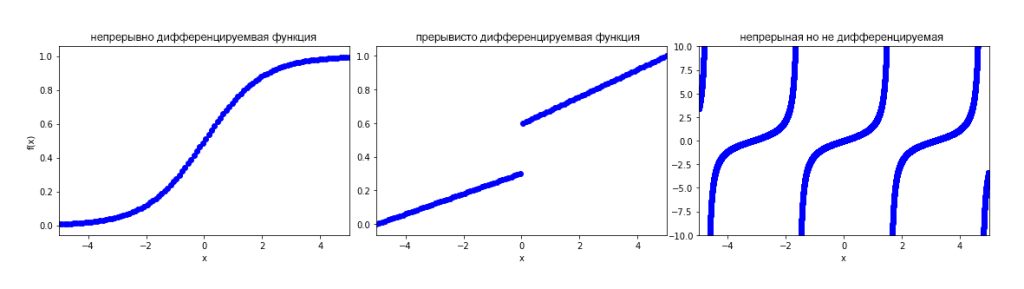
Если изучаемая нами функция удовлетворяет условию непрерывной дифференцируемости, то нейронные сети могут аппроксимировать ее (упростить, найти приближённые значения), по существу вычисляя ее разложение Тейлора. Однако, хотя доказано, что нейронные сети могут аппроксимировать любые непрерывно дифференцируемые функции, нет никакой гарантии, что конкретная сеть когда-либо сможет изучить это приближение.
Учитывая конкретную инициализацию весов, может оказаться невозможным изучить эту аппроксимацию с использованием минимизации функции потерь и обратного распространения ошибки.
В конечном итоге сеть может застрять на локальном минимуме и, возможно, никогда не сможет повысить свою точность выше определенного порога.
Это приводит к существенному недостатку нейронных сетей: они чувствительны к начальной рандомизации их весовых матриц.
Теорема о бесплатном обеде
Еще одна важнейшая теорема машинного обучения гласит, что любой данный алгоритм может хорошо решать некоторые классы задач, но не может решить некоторые другие классы вообще.
Это означает, что для любой данной задачи конкретная архитектура нейронной сети может быть эффективной, в то время как другая не будет функционировать должным образом, если вообще будет работать.
Давайте посмотрим, что это значит, сравнив персептроны и глубокие нейронные сети в решении одной и той же задачи.
Основной тип задач, в решении которых нейронные сети особенно хороши – это так называемые линейно неотделимые задачи. Первые нейронные сети были специально разработаны для решения одной из них, учитывая неудачу в этом смысле их родственников-персептронов. Этой проблемой было изучение функции XOR для двоичных переменных, графическое представление которой:
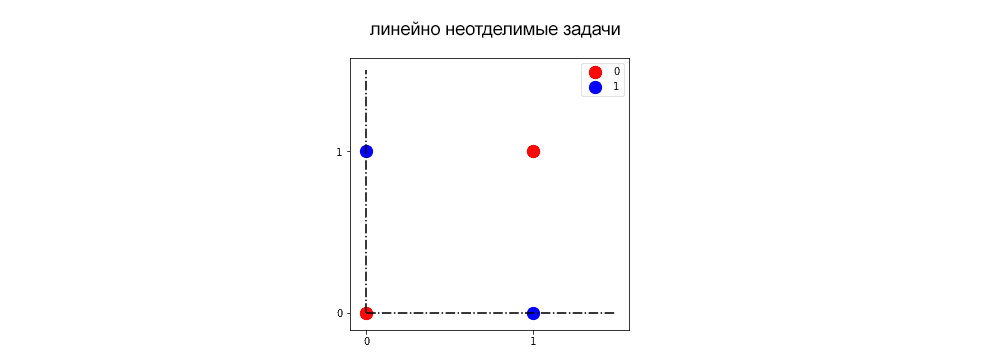
Нейронные сети могут изучать разделяющую гиперплоскость для классификации красных и синих значений, в то время как персептроны не могут. Одна из таких гиперплоскостей (пунктиром) – та, которую мы видим на следующем графике:
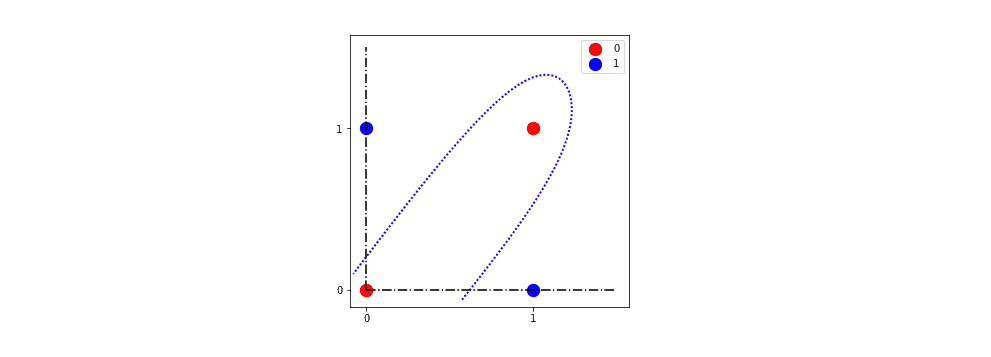
Другой способ взглянуть на эту идею заключается в том, что если мы не можем спроецировать проблему на гиперплоскость, в которой решение линейно разделимо, то персептроны, сами по себе являющиеся одним из вырождающихся видов нейронных сетей, не решат ее. В то же время глубокие нейронные сети, другой тип нейронных сетей, смогут решить эту проблему.
Это частный случай более общего правила.
Если один алгоритм машинного обучения эффективен при решении одного класса задач, он будет неэффективен при решении всех остальных.
Таким образом, чтобы обойти эту проблему, необходимо иметь хорошее теоретическое представление о машинном обучении в целом и знание эвристики, связанной с решением любой данной задачи в частности.
Данные и вычислительная мощность
Внедрение искусственного интеллекта и в частности для обучения нейронных сетей требуются, по сравнению с другими алгоритмами машинного обучения, значительно большие наборы данных. Для обучения им также требуются значительные вычислительные мощности.
Проблема возникает тогда, когда набор данных или размер нейронной сети становятся слишком большими. Нейронные сети обычно плохо масштабируются по мере увеличения объема данных или количества их слоев и нейронов. Есть несколько факторов, которые вызывают такое поведение:
- Нейронные сети часто имеют нелинейные функции активации. Градиенты нелинейных функций активации дорого вычислять при обратном распространении ошибки
- Порядок, в котором мы отправляем обучающие данные в нейронную сеть, влияет на результат. Нейронные сети, как правило, часто достигают локальных минимумов своей функции потерь. Способ обойти это – обучить сеть несколько раз на случайных пакетах обучающего набора данных, но для этого требуется многократно увеличить попытки обучения
- Другая проблема касается весов сети. По мере увеличения размера нейронной сети весовые матрицы масштабируются быстрее, чем линейно
- Наконец, не все архитектуры нейронных сетей одинаковы. Разные архитектуры могут решать одну и ту же задачу с сопоставимой точностью, требуя при этом существенно разного объема вычислений. Это означает, что мы часто ищем наиболее эффективную архитектуру методом проб и ошибок.
Поиск аналитических (алгоритмических) способов решений различных задач
Есть и еще один серьезный недостаток в использовании нейронных сетей. На этот раз проблема больше связана с предвзятостью скептиков, чем с реальными фактами :).
Машинное обучение является чрезмерным и ненужным для многих распространенных задач.
Это не имеет никакого отношения к нейронным сетям в частности, но это общая проблема, которая затрагивает сообщество специалистов по обработке данных и приводит к чрезмерному использованию нейронных сетей.
Слишком частый случай неправильного применения нейронных сетей – это ситуации, когда вместо ИИ мы можем решить проблему с помощью простых математических алгоритмов.
Сегодня эта проблема широко распространена в индустрии машинного обучения, но ее часто игнорируют. Давайте возьмем в качестве примера следующую проблему:
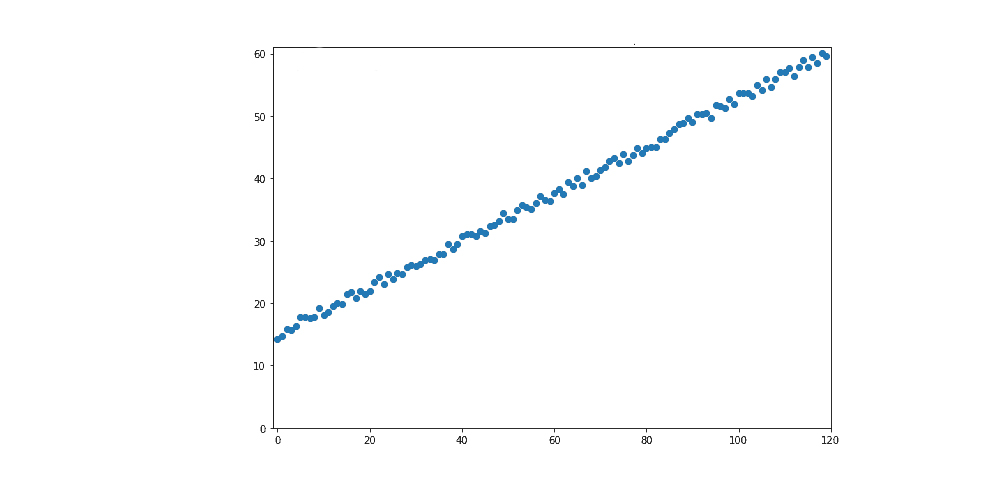
В этой задаче автомобиль движется по улице с постоянной скоростью.
Наша цель – предсказать его местоположение на более позднее время, . Для этого мы сначала измеряем его положение через несколько интервалов и получаем измерения, показанные на изображении выше.
Результатом является достаточно большой набор данных, к которому мы затем применяем нейронную сеть для линейной регрессии. Набор данных на изображении выше включает ошибки в измерениях, как и в любых реальных наборах данных.
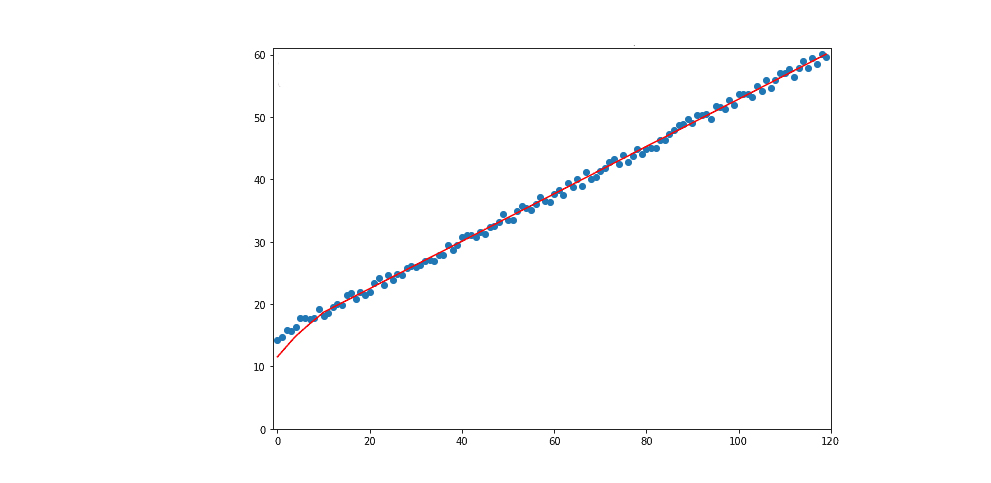
Затем мы разделяем набор данных на обучающий и тестовый наборы данных. На обучающем наборе данных мы обучаем глубокую нейронную сеть и измеряем ее точность по сравнению с тестовым набором данных. После нескольких тысяч эпох обучения сеть узнает, что существует следующая взаимосвязь между временем ввода и положением вывода
:
Красным показано как нейросеть предсказывает дальнейшее поведение автомобиля.
По возможности надо находить алгоритмические решения
Как это обычно бывает в задачах машинного обучения, мы могли бы измерить точность нашей системы.
Если бы мы сейчас измерили бы точность, то получили бы очень хороший результат на котором можно было бы и остановиться. НО!
Базовые знания в области физики дадут возможность решить эту задачу гораздо проще. Поскольку скорость постоянна, то и
, которые мы можем вычислить вручную.
Случаи, подобные этому, совсем не редкость на практике, и мы должны иметь их в виду.
Решая новую проблему, мы не должны сразу пытаться использовать машинное обучение.
Если алгоритмические решения неизвестны, только тогда мы должны рассмотреть возможность применения в первую очередь более простых алгоритмов машинного обучения, а во вторую очередь нейронных сетей.
В этом материале мы рассмотрели некоторые причины, по которым мы должны или не должны применять нейронные сети для наших задач.
Из-за теоремы об универсальной аппроксимации мы знаем, что нейронная сеть может аппроксимировать любые непрерывно дифференцируемые функции.
Это, как правило, справедливо не для всех алгоритмов машинного обучения и является существенным преимуществом нейронных сетей в частности.
Теорема о том, что бесплатных обедов не бывает, говорит нам, что некоторая сетевая архитектура будет лучшим решением данной проблемы.
Мы также знаем, что та же архитектура не будет оптимальным решением для других задач.
Из-за чрезмерного объема данных и вычислительной мощности, доступных сегодня, нейронные сети становятся все более распространенными.
Нам следует использовать другие алгоритмы машинного обучения, если данных или вычислительной мощности недостаточно.


